作者:xiph.org(原文链接)
翻译:刘通
原标题:RNNoise: Learning Noise Suppression
前文连接:RNNoise:用深度学习进行噪声抑制(基础知识)
一个混合方法
感谢深度学习,现在把深度神经网络抛给整个问题是很流行的做法。这个做法叫做端到端—一路下去都是神经元。端到端方法已经在语音识别和语音合成中得到了应用。一方面,这些端到端系统证明了深度神经网络是多么强大。另一方面,这些系统有些时候可能都是次优的,而且会浪费资源。举个例子,一些噪声抑制的方法使用具有数千个神经元的层来进行去噪。缺点不仅在于运行网络的计算成本,模型本身的大小也是缺点之一,因为你的库现在有几千行代码和几十兆字节的神经元重量。
这就是我们为什么在这里使用一个不同的方法的原因:保留所有基本的信号处理过程,但是让神经网络学习除信号处理以外所有需要不断调整的棘手部分。另外一个与部分已有深度学习噪声抑制所不同的地方在于我们把目标设为实时通信而不是语音识别,所以我们无法往前获取几毫秒的内容。
定义问题
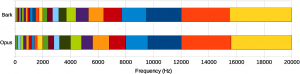
为了避免存在太大量的输出—也就是大量的神经元—我们决定不直接使用采样点或者频谱。而是我们考虑遵循Bark量表的频带。我们总共使用22个频带,而不是480个(复数)频谱值。
Opus频带和实际Bark量表的对比。对于RNNoise来说,我们使用与Opus同样的基本布局。因为我们将频带重叠起来,所以Opus频带之间的界限就是重叠的RNNoise频带的中间值。频带在高频的时候更宽,这是因为在频率高的时候人耳对频率的分辨率相对更低。在低频区域,频带更窄,但是并没有Bark那么窄,是因为如果太窄的话我们就没有足够的数据来进行良好的估计了。
当然,我们不能只从22个频带中的能量重塑音频。我们可以做的是计算对每个频带来说可用于信号的一个增益。你可以想成我们使用一个22段的均衡器,并且迅速改变每个频带的电平增益以达到降低噪声保留信号的功能。
使用每频带增益有几个好处。第一,因为我们需要计算的频带数少了,所以这么做可以建成一个简单的多的模型。第二,这么做不可能产生音乐噪声效应,这种效应是只有一个音调通过而周围的音调都被衰减掉。音乐噪声在噪声抑制中很常见,并且十分烦人。有了足够宽的频带,我们要么让这个频带都通过,要么把整个频带都去掉。第三个好处来源于我们如何优化模型。因为增益永远是在0到1之间,所以我们可以简单统括使用一个正弦激活函数(输出也是0到1之间)来计算他们以确保我们不会犯下非常愚蠢的错误,比如在之前并不存在噪声的地方认为的添加上噪声。
我们使用频带而导致的低分辨率的缺点是我们没有足够高的分辨率来抑制音调谐波之间的噪声。幸运的是,这其实并不重要,而且还有一个简单的技巧来完成这个工作(详见下文音调滤波部分)。
因为我们是基于22个频带计算得来的输出,所以输入频率有更高的分辨率是没有意义的,所以我们使用同样的22个频段将频谱信息送入神经网络。因为音频有很大的动态范围,所以计算能量的对数值要比直接使用能量值要好。而在我们这么做的时候,它永远不会用DCT去除相关的特征。所得数据是基于Bark量表的倒谱,其余MFCC密切相关,与语音识别中使用的非常相似。
处了我们的倒谱系数以外,我们还包括:
#前6个跨帧系数的一阶导数和二阶导数
#音调中期
#音调增益
#用于语音检测的特殊非平稳度值
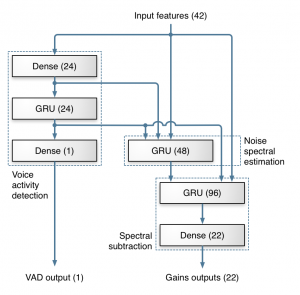
这使得神经网络共有42个输入特征。
深层结构
我们使用的深层结构的令该来源于传统噪声抑制方法。大部分的工作是由3个GRU层完成的。下图展示了我们用来计算频带增益的层,以及结构如何映射到噪声抑制的传统步骤。当然,像神经网络的通常情况一样,我们没有办法证明网络像我们设想的那样使用层。但是事实上,这个拓扑结构比我们试过其他的结构都要好,所以我们有理由认为它的确是按照我们所设计的方式工作的。
完全取决于数据
甚至深度神经网络有的时候也很“笨”。他们在他们知道的方面可以获得非常好的结果,但是他们在输入值与他们所知道的差距太远的话就可能发生错误。甚至更糟的是,他们与那些特别懒的学生一样。如果他们在训练过程中有任何可以偷懒的地方以避免学习困难,那他们一定会抓住这个机会。这就是为什么训练数据的质量至关重要的原因。
在噪声抑制情况中,我们不能够只收集可用于监督学习的输入/输出数据,因为我们几乎不可能同时获得干净的话音和含噪的话音。相反,我们必须从清晰话音和噪音的记录中人为的创建数据。棘手的部分是获得各种各样的噪声数据以添加进噪声中。我们还必须确保覆盖各种记录条件。举个例子,之前只是基于全带(0-20kHz)音频训练的版本在处理低频滤波产生的0-8kHz的音频是会出现错误。
音调滤波
因为我们的频带分辨率太过粗糙,无法滤除音调谐波之间的噪声,所以我们进行基本的信号处理。这是混合方法的另一个部分。当有相同变量的多个测量值时,提高精度(降低噪声)的最简单的方法就是计算平均值。显然的是,只是计算相邻音频采样点之间的平均值并不是我们想要的。但是,当信号是周期的时候,那么我们可以计算由音调周期偏移样本的平均值。结果是梳状滤波器可以使音调谐波通过,并且削减他们之间的频率—也就是存在噪声的地方。为了避免产生失真,梳状滤波器独立的应用在每个频带中,它的滤波程度同时取决于音调相关以及神经网络计算得来的频带增益。
在原网页中有非常好的demo,请点击此处跳转原文以运行demo。